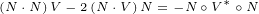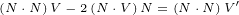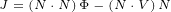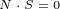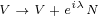Maxwell equations in 8D
Abstract
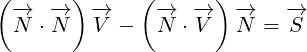 |
To read this article you will need basic knowledge about geomteric algebra. At the
beginning of this article I am going to write equations that are describing reflection of
a vector in 3D. I am going to show that these equations are valid also for
4D multivector (scalar + vector) and 8D multivector (scalar + vector +
pseudoscalar + pseudovector). So, we can generalize and say that we have
a definition for multivector reflection (3D, 4D or, in most general case,
8D).
Then, I am going to show that 4D multivector reflection can be used to represent
famous Maxwell equations. This is not surprising. After all, Maxwell equations
are Lorentz invariant. And 4D reflection is just a statement about Lorentz
invariance. So, it makes sense that 4D multivector reflection describes Maxwell
equations.
I am not an expert in physics, in fact I am total amateur. I know about Covariant
formulation of classical electromagnetism. But in this article there are no matrices and
tensors, no covariant and contravariant objects, no lower and upper indices. There is
only multivectors. There is nothing about electric and magnetic fields. Only
objects that will be used in this article is Electromagnetic four-potential and
Four-current. Maxwell equations in this article are written using only 4D
multivectors.
Lorentz invariance can be interpreted as a fact that we live in 4D world. But, if we
follow logic (and nature for sure follow it), then it should not be 4D world. It should be
8D world, simply because multivector has 8 components.
This is nothing new actually. Famous Dirac equation has bispinor as its main
object, and bispinor is 4D complex vector, which is essentially 8D component object.
But Dirac equation is derived from energy-momentum relation 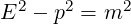 . It has
. It has
mass term and it is more complicated than Maxwell equations. What I want to do in
this article is much simpler. I want to extend Maxwell equations to 8D multivectors.
There is no mass term in this article, as there is no mass term in ordinary Maxwell
equations.
Perhaps this article is not of any significance. This is more mathematics, than
physics. But generalization can lead to new discoveries, and that is what I am trying to
do in this article. I am trying to generalize Maxwell equations and write something
that we can call Maxwell equations in 8D. Perhapse someone, with more
knowledge and skill than myself, can extend my work and find some physical
interpretation.
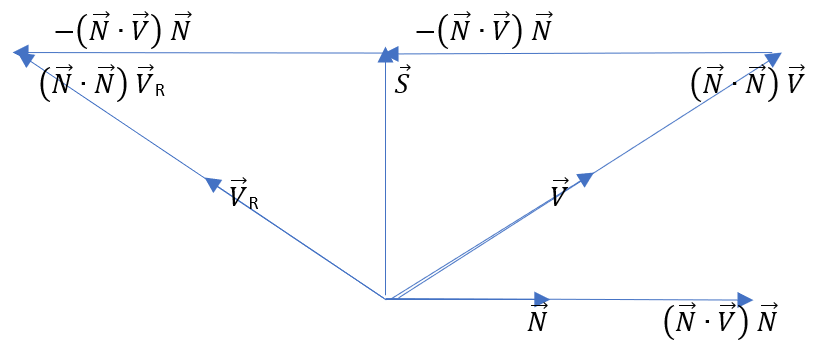
1 Reflections in 3D
Reflection of 3D vector can be represented by using geometric algebra. This is well known
fact, and it is shown in Annex A. Here I will just write the main equations and I will try to
explain their geometrical meaning.
| (1.1) |
| (1.2) |
Vector  is reflected to vector
is reflected to vector 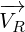 . Vector
. Vector 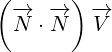 is reflected to vector
is reflected to vector
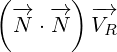 .
.
Vectors 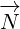 and
and 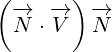 are perpendicular to reflection surface. Vector
are perpendicular to reflection surface. Vector 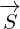 is
is
vector that lies inside reflection surface and it is halfway between vectors 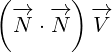 and
and
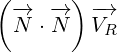 .
.
Equation 1.1 describes reflection, so we can call it Reflection equation. Equation 1.2
introduces surface vector 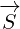 , so we can call it Surface equation.
, so we can call it Surface equation.
Why do we need vector 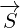 ? You can see from the figure 1 that vectors
? You can see from the figure 1 that vectors 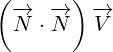 ,
,
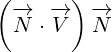 and
and 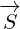 form a right triangle. This is easy to prove if you inetrpret scalar
form a right triangle. This is easy to prove if you inetrpret scalar
product of two vectors as a cosine of the angle between them multiplied by their lengths.
But I don’t want to loose time to prove it. I am more intersted in the geometry that is
described by equation 1.2. Basically, scalar products 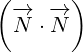 and
and 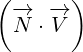 are scaling
are scaling
original vectors 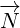 and
and 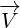 in a proper way so that they form a right triangle with surface
in a proper way so that they form a right triangle with surface
vector 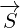 .
.
In fact, equation 1.2 is more important for us than equation 1.1 and we are only going to
use equation 1.2 for the rest of this article.
I hope I explained you the geometric interpration of equations 1.1 and 1.2. If you
understood it, than you understand the basic idea behind this article. We will talk later
about 4D vectors and 8D vectors, but that will only add some more complicated
mathematics, basic idea represented by figure 1 still remains the same!
1.1 Continuity equation
Vectors  and
and 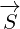 are perpendicular. It is easy to prove. We start from Surface equation
are perpendicular. It is easy to prove. We start from Surface equation
1.2:
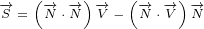 |
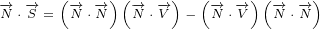 |
| (1.3) |
We will call equation 1.3 the Continuity equation. It will become obvious
why we call it like that in the next section when we make analogy to Maxwell
equations.
1.2 Gauge invariance
One more note is needed that is very important for the rest of this article. If we translate
vector 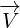 by some vector that is normal to reflection surface, then vector
by some vector that is normal to reflection surface, then vector 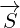 is
is
not changed. We call this fact Gauge invariance. Again, it will become obvious
why we call it like that in the next section when we make analogy to Maxwell
equations.
Here is the figure and equations that describe Gauge invariance in 3D:
| (1.4a) |
| (1.4b) |
So, we are saying that surface equation 1.2 is still valid after the transformation done by
equaiton 1.4a. This is easy to prove:
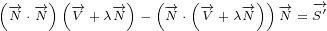 |
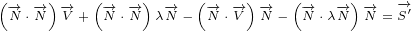 |
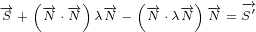 |
| (1.4c) |
Last equation is equal to 0, since 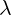 is scalar.
is scalar.
Equation 1.4a we will call Gauge transformation and equation 1.4b we will call
Gauge invariance equation.
Equation 1.4c looks pretty trival. It involves only one vector 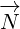 and one scalar
and one scalar 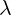 . It
. It
is obviously true, since you are free to change place of the scalar 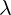 . But things will get
. But things will get
complicated later and this equation will be important for us. We will call it Gauge
simplified equation.
That is it for this section. I hope you understood geometry between equations 1.1, 1.2,
1.3 and 1.4. I hope you understood it very well. In fact, I hope you understood it so well,
that you can call them very stupid equations!
After all, if we for the moment ignore scalar products (which are there only to scale
original vectors in a proper way), these equations tell us very simple geometrical facts. For
example, equations 1.4 are basically telling us that if we translate vector 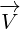 paralell to x
paralell to x
axis, then its height (which is vector  ) will not be changed. But this is so simple fact
) will not be changed. But this is so simple fact
that it can be understood by the kindergarten children!
2 Reflections in 4D
If we add scalar component to 3D vector, then we get multivector that has 4 components. In
the geometric algebra language, multivector with scalar and vector components is called
paravector. We will call it 4D multivector.
It is shown in Annex B that all equations from previous section are true for 4D
multivector also! I think this is remarkable fact! If you pause and think about it for the
moment, what we have is a set of equations that are true both for 3D and 4D vectors. So,
geometrical intuition that we have about 3D vectors (as a human beings that think are
living in 3D world), we can use to better understand 4D world that we actually live
in!
It is important to note that scalar product of two 4D multivectors is not the same as
scalar product of two 3D vectors. This is already explained in Annex B, but we will repeat it
here for easier reference. So, for 4D multivectors, scalar product is given by following
equation:
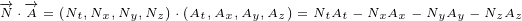 |
We can also write:
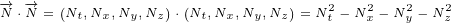 |
Now we are going to repeat equations from previous section.They all have the same
form.
Surface equation 1.2 is the same:
| (2.1) |
Continuity equation 1.3 is the same:
| (2.2) |
Gauge equations 1.4 are the same:
That is all. All we did is to generalize the scalar product definition so it can be
applied to 4D vectors, and now we can use equations 2.1, 2.2 and 2.3 to describe 4D
world!
3 Maxwell equations in 4D
Let us use following replacements:
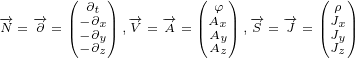 |
(3.1) |
So, we introduced three new 4 D multivectors. Multivector 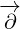 has, as components,
has, as components,
partial derivatives with respect to time and space (notice the minus sign on space
derivatives). Multivector 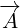 you can recognise as a Electromagnetic Four-potential.
you can recognise as a Electromagnetic Four-potential.
Multivector 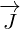 you can recognise as a Four-current.
you can recognise as a Four-current.
With replacements defined by equation 3.1, surface equation 2.1 becomes:
| (3.2) |
This equation is actually Maxwell equation written in the form of multivectors! Let us
expand this equation to prove it:
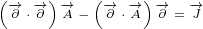 |
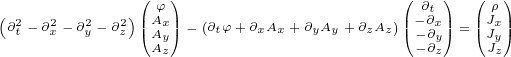
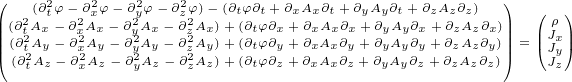
What shoud we do with terms like 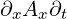 ? The rule we are going to adapt is to treat
? The rule we are going to adapt is to treat
them like simple multiplication where you can do the multiplication in any order.
After all, you are allowed to switch the order of partial derivatives (if the function
and its derivatives are continuous and differentiable at the point of interest). For
example:
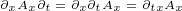 |
So, we can say:
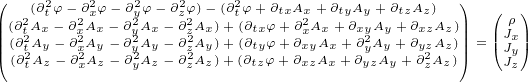
You can check yourself that above expanded version of our surface equation 3.2 is
equivalent to Maxwell equations.
There is one important step that we did but did not talk about. We have moved from
space of real numbers to the space of real functions. In previous section, vectors
 ,
,  and
and 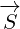 were vectors that are represented by 4 real numbers. Now,
were vectors that are represented by 4 real numbers. Now,
vectors 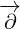 ,
, 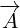 and
and 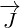 are vectors represented by 4 real functions. For example
are vectors represented by 4 real functions. For example
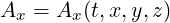 . So, in this section, when we say scalar we do not think of
. So, in this section, when we say scalar we do not think of
simple real number, but we think of scalar function. But this does not change
our intuitive understanding of Maxwell equations as multivector reflections in
4D.
Continuity equation 2.2 becomes:
| (3.3) |
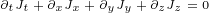 |
Well, this actually is Continuity equation that describes conservation of electrical
charge!
Let us see how will 4D Gauge equations 2.3 look now:
Equation 3.4a you can recognise as the definition of gauge transformation that leaves
Maxwell equations invariant. Parameter 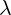 is scalar function (as we already said, in this
is scalar function (as we already said, in this
section we are working in the space of real functions), as required by Maxwell equations
gauge transformation.
This is remarkable result! Everything works automatically! We did not change equations
for 4D reflection in any way. Only thing we did is to use replacements 3.1, and we got
Maxwell equations, with Continuity equation and Gauge transformation for free! So,
Maxwell equations can be understood as 4D reflection!
Equation 3.4c is correct, because 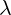 is scalar. This is not trivial anymore, like it was
is scalar. This is not trivial anymore, like it was
with equation 2.3c where 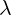 was simpe number. Now
was simpe number. Now 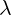 is scalar function and
is scalar function and 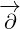 is
is
multivector with derivative operators as components. Still, it can be easily verified that
equation 3.4c is true by expanding it in the same way as we expanded Maxwell equations
3.2.
4 Reflections in 8D
General multivector has 8 components – 1 for scalar, 3 for vector, 3 for pseudovector and 1
for pseudoscalar. Does the equations we have written in section 1 hold in general
case of multivector with all 8 components? Yes they do, as it is shown in Annex
C!
Since we work in 8D, things are more complicated. For us humans at least, it is easier to
think of 8D multivector as sum of two 4D vectors:
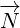 ,
, 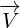 and
and 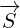 are 8D multivectors, and
are 8D multivectors, and 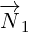 ,
,  ,
, 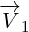 ,
, 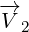 ,
, 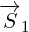 and
and
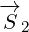 are 4D multivectors. Symbol
are 4D multivectors. Symbol  represents basis for the pseudoscalar component:
represents basis for the pseudoscalar component:
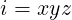 . By multipling 4D vector that has scalar and vector component with
. By multipling 4D vector that has scalar and vector component with  , we get
, we get
pseudoscalar and pseudovector components.
Equation for scalar product of two 8D multivectors can be written by using scalar
product of 4D multivectors:
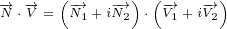 |
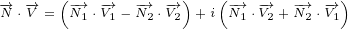 |
We can also write:
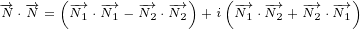 |
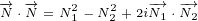 |
By moving from 4D to 8D we are actually moving from real numbers to complex
numbers. As you can see from above equations, scalar product in 8D has scalar
and pseudoscalar component, so it can be think of as a complex number. Also, if
we consider usual definition that the scalar product of multivector by itself is
multivector length squared, we can see from above equations that multivector length in
8D is complex number. So, it becomes obvious that, in 8D world, the most basic
element is not a real number, but it is complex number (scalar + pseudoscalar
component).
There is no difference between equations for 4D and equations for 8D. We can repeat
equations 2.1, 2.2 and 2.3 here, since they would have the same form.
But, we will write equations in 8D by expanding 8D multivectors to two 4D multivectors.
Here are these expanded versions.
Surface equation 2.1 becomes:
| (4.2) |
Continuity equation 2.2 becomes:
 |
| (4.3) |
For the gauge equations, we will represent parameter 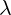 as complex number. So, we will
as complex number. So, we will
replace 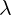 with
with 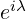 .
.
So, by using replacement equations 4.1, and by using 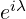 instead of
instead of 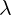 , gauge
, gauge
equations 2.3 become:
Equations for 8D multivector reflection are longer and take more time to write compared
to 4D multivector reflection equations, but basically all we did is to change real numbers
with complex numbers. And now we can use equations 4.2, 4.3 and 4.4 to describe 8D
world!
5 Maxwell equations in 8D
Here are replacements that we are going to use in this section:
| (5.1) |
Multivector 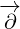 is the same multivector we used before in the section about Maxwell
is the same multivector we used before in the section about Maxwell
equations in 4D.
Multivector 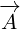 is also the same, it is Electromagnetic Four-potential. Notice
is also the same, it is Electromagnetic Four-potential. Notice
that, in the section about Maxwell equations in 4D, multivector 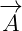 was part
was part
of the multivector 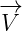 that was rotated, and now it is part of the multivector
that was rotated, and now it is part of the multivector
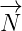 .
.
Multivector 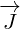 is not Four-current anymore. In this section it is used as a new 8D
is not Four-current anymore. In this section it is used as a new 8D
multivector that does not have any known physical meaning.
Multivector 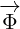 is also new. It represents 8D multivector that is rotated.
is also new. It represents 8D multivector that is rotated.
Let us write surface equation 4.2 with replacements definied in equation 5.1.
We will only expand multivector 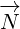 . Multivectors
. Multivectors 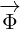 and
and 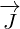 will not be
will not be
expanded. In this way equations will be much shorter to write and much easier to
understand.
| (5.2) |
Equation 5.2 is our Maxwell equation in 8D! This equation is not different from surface
equations we have written so far. For example, if you compare it to 3D surface equation 1.2,
form is the same. We have only replaced vectors 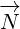 ,
, 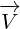 and
and 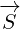 with
with 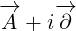 ,
, 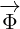
and 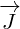 . So, it is still surface equation, and the geometrical interpretation is the same as
. So, it is still surface equation, and the geometrical interpretation is the same as
described in section 1.
But why we put multivector 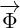 inside a box? The answer is simple, in this way we are
inside a box? The answer is simple, in this way we are
saying that partial derivative acts only on components of 8D multivector 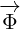
.
Of course, immediately you have another equation – why partial derivatives do
not act on components of 4D multivector 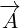 ? This cannot be answered in one
? This cannot be answered in one
sentence.
5.1 What are partial derivatives acting on?
Partial derivatives are making things more complicated. They are not simple functions that
you can multiply with other functions in any order. They are actually operators that must
act on some other function. And we must put some rule to answer what that function is. It
is not easy to come up with that rule, because we do not have some final result that we can
use to validate it.
If we would expand this equations, there would be many products like this one for
example:
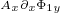 |
We are not sure if partial derivative 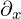 acts on
acts on 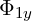 or
or 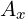 or both. So, the question
or both. So, the question
is: What are partial derivatives acting on?
When we expanded 4D Maxwell equation 3.2, we said that the order of multiplication is
not important. But, Maxwell equations had only one variable, 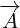 , so it was easy to answer
, so it was easy to answer
this question: they were acting on 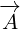 .
.
But, now we have two variables, 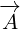 and
and 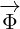 , so now we are not sure if partial
, so now we are not sure if partial
derivative 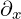 acts on
acts on 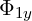 or
or 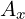 or both.
or both.
My answer to this question can be found at the beginning of Annex C. I will not go into
all the details how we derived reflection equations for 8D multivectors, but the beginning of
this derivation is important now. At the beginning of Annex C we have used geometric
products:
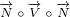 |
Let us use replacements defined in the equation 5.1 with above equation, and see what
we get:
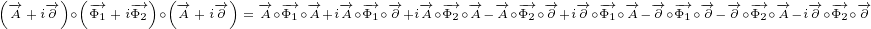 |
We can see that 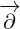 always directly multiplies
always directly multiplies 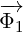 or
or 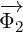 , it never directly multiplies
, it never directly multiplies
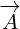 . This is the reason why
. This is the reason why 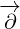 never acts on
never acts on 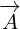 . If we would continue to expand above
. If we would continue to expand above
geometric products, at the end, after very complex manipulations that are done in Annex C,
we would obtain our 8D Maxwell equation 5.2. But all that manipulations does not change
the fact that 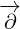 never directly multiplies
never directly multiplies 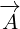 . The order of the multiplication that we got
. The order of the multiplication that we got
at the end (equation 5.2) is not important, but the order of the multiplication at the
beginning is important!
5.2 Gauge invariance for Maxwell equations in 8D
This is most important part of this article.
5.2.1 Gauge invariance for Maxwell equations in 8D – preparation
Calculations for gauge invariance for Maxwell equations in 8D will be far from easy. We need
to be well prepared.
We need to analyze partial derivatives on the terms that will later show up in our
calculations:
Looking at the last equation 5.3f, we can see that 3rd and 4th terms cannot be added
together because they are asymmetric, they have different partial derivatives acting on
different symbols. For these terms we need to mark which derivative acts on which
symbol.
It is hard to explain this with words only. It is best to look at some examples. Here is
one example:
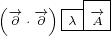 |
In above example there is no problem, because we do not have mixed partial derivatives.
One partial derivative will act on 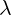 term, and second on
term, and second on 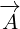 , but they are always going
, but they are always going
to be partial derivatives with respect to same parameter ( or
or 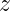 ). We
). We
know how to interpret expanded terms, for example: 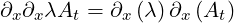
.
Here is another example:
 |
In above example we have a problem, because we have mixed partial derivatives. One
partial derivative will act on  term, and second on
term, and second on 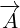 , but we do not know which
, but we do not know which
derivative acts on which symbol. We do not know how to interpret expanded terms, for
example:  . Here we are not sure which derivative acts on
. Here we are not sure which derivative acts on 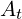 and which on
and which on 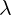
.
So, better way to write above example is this:
 |
We have marked partial derivatives with subscript, so now we know how to interpret
expanded terms. For example: 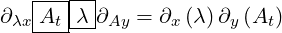 .
.
Here is another example:
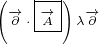 |
Above example does not have a problem. We have mixed partial derivatives, but they act
on one symbol only. So, for terms like this one, we do not need to use subscript on
derivatives.
One more thing. We are going to use double boxes in case both derivatives
act on same symbol. Number of boxes in each term must be equal to number of
derivatives in that term. This rule can help us to validate our work, because things
are getiing very complicated. So, last example we are going to write in this way
actually:
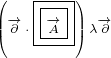 |
Just to be clear, following two examples are not the same:
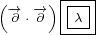 |
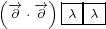 |
First example involves second order derivatives 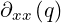 . Second example involves
. Second example involves
product of two first order derivatives 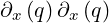 .
.
5.2.2 Gauge invariance for Maxwell equations in 8D – equations
Let us see what are the gauge transformations for 8D Maxwell equations. We will also
repeat gauge transformations for 3D and gauge transformations for 4D Maxwell equations,
so we can compare all of them.
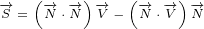 |
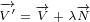 |
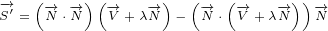 |
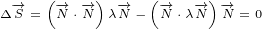 |
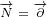 |
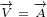 |
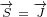 |
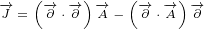 |
 |
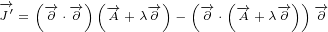 |
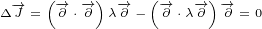 |
8D Maxwell gauge equations 5.6 look very complicated. But all we did is to replace 
with  ,
,  with
with 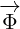 and
and 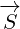 with
with 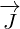 , and we have replaced scalar function
, and we have replaced scalar function
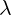 with complex function
with complex function 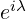 .
.
We already explained why multivector  is boxed in the equation 5.6a. When we make
is boxed in the equation 5.6a. When we make
replacement defined with equation 5.6b into equation 5.6a, we end up with equations 5.6d
and 5.6e, that have on some places multivector 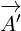 boxed, and on some places multivector
boxed, and on some places multivector
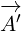 not boxed. But there is no problem with that. We are just making replacements, and
not boxed. But there is no problem with that. We are just making replacements, and
we are keeping consistency.
For the 8D Maxwell gauge equations, we will also transform multivector 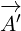 , with the
, with the
same transformation that is done for the 4D Maxwell gauge equations. But 8D equation for
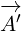 , equation 5.6c, has one small difference compared to 4D equation. It has
, equation 5.6c, has one small difference compared to 4D equation. It has
subscript on the partial vector 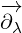 . This means that, when this term is multiplied
. This means that, when this term is multiplied
with other terms, this partial vector will act only on scalar function 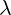 next to
next to
it.
3D gauge and 4D Maxwell gauge look trivial. We definitely cannot say that about 8D
Maxwell gauge.
5.2.3 Gauge invariance for Maxwell equations in 8D – calculation
Let us repeat equation 5.6e one more time here:
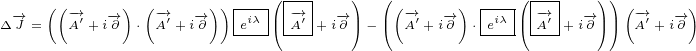 |
For the derivation we will use equations 5.3.
The important thing is that we must be careful where boxes are placed. There will be
terms that are different only in placement of boxes, and for that reason they cannot cancel
each other.
Scalar terms 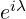 and
and  are free to change places.
are free to change places.
Let us start. Equation 5.6e has 2 big terms. Each of them has 8 smaller terms. We can
write:
Equation  was derived using equation 5.3e. Equation
was derived using equation 5.3e. Equation  was derived using equation
was derived using equation
5.3f. Equation  has two terms where we had to mark derivatives with subscript because
has two terms where we had to mark derivatives with subscript because
of mixed partial derivatives.
We can write:
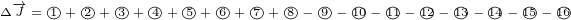 |
Next we can subtract similar terms:
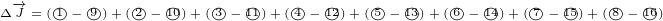 |
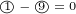 |
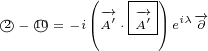 |
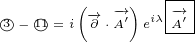 |
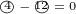 |
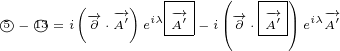 |
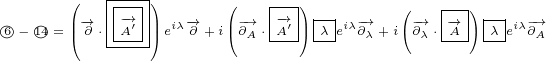 |
 |
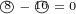 |
Finally we can sum everything together. We can also group similar terms together. We
can say that for 8D Maxwell equations delta current is not zero, as it is for 4D Maxwell
equations. 8D delta current has real part and imaginary part. So, we can write:
Imaginary delta current has terms with 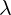 symbol. We need to make replacement for
symbol. We need to make replacement for
multivector 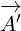 and see if it will cancel these terms.
and see if it will cancel these terms.
| (5.9) |
Real delta current is:
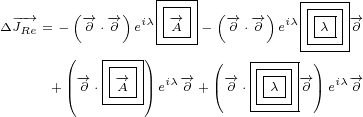 |
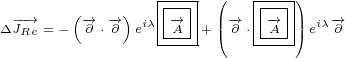 |
Imaginary delta current is:
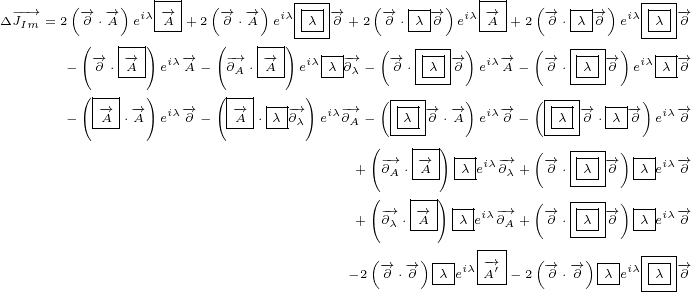 |
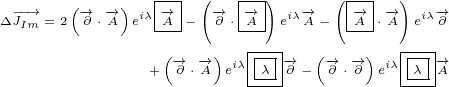 |
Looking at the real delta current, we can recognize Maxwell equation current.
Imaginary term is something new. We can split it into two parts. Let us introduce some
new definitions, and write delta current using these new definitions:
| (5.10) |
| (5.11) |
| (5.12) |
| (5.13) |
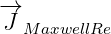 is Maxwell current. We will call it Maxwell real current, since it belongs to
is Maxwell current. We will call it Maxwell real current, since it belongs to
real part of delta current  .
. 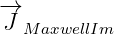 is similar to Maxwell current. We will call it
is similar to Maxwell current. We will call it
Maxwell imaginary current, since it belongs to imaginary part of delta current  .
.
 depends on scalar term
depends on scalar term 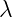 , so we will call it Maxwell scalar
, so we will call it Maxwell scalar
current.
We did not get zero for delta current. First impression is not good. Delta current
depends both on potential vector 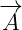 and on scalar term
and on scalar term 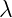 . But still, results are very
. But still, results are very
interesting.
Maxwell real current and Maxwell imaginary current depend on potential vector 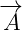 .
.
This is interesting, because we got something new, we got Maxwell imaginary current.
It is very similar to Maxwell real current. Since Maxwell real current represent
Four-current, then maybe Maxwell imaginary current has some physical interpretation as
well.
Maxwell scalar current depend on potential vector 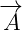 and on scalar term
and on scalar term 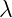 . But it is
. But it is
not so bad, because we have derivatives only on 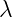 term. There are no derivatives on
term. There are no derivatives on
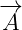 .
.
6 Analyzing Maxwell currents in case of radial potential
In this section we will say that potential vector function 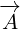 and scalar function
and scalar function 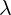 are
are
radial, which means that, in each 4D point, their value depends only on value and direction
of distance vector 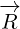 .
.
We can express this in following way:
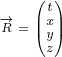
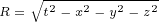 |
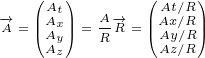
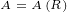 |
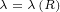 |
Calculation will be easier with following helper variable:
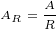 |
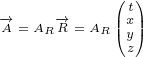
We will need following first order derivatives:
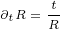 |
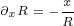 |
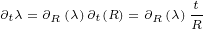 |
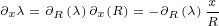 |
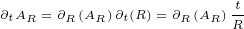 |
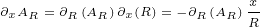 |
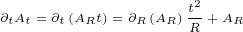 |
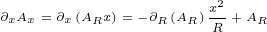 |
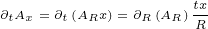 |
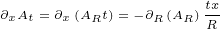 |
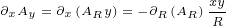 |
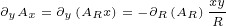 |
We will also need following first order derivatives:
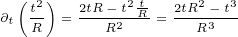 |
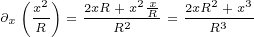 |
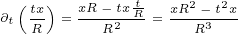 |
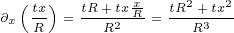 |
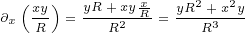 |
We will need following second order derivatives:
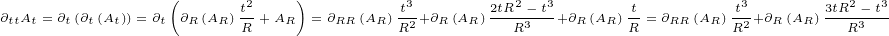 |
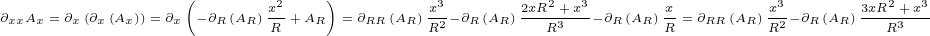 |
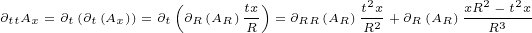 |
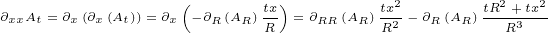 |
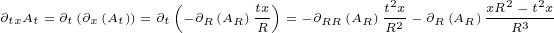 |
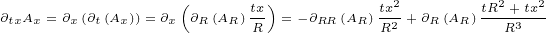 |
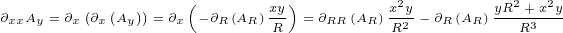 |
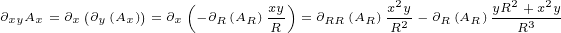 |
We are ready to calculate delta currents. We will calculate only the first vector
components, because it is enough to deduce the result (since the result must be radial
function as well).
At the end we get following equations if  is radial vector:
is radial vector:
| (6.2) |
| (6.3) |
| (6.4) |
| (6.5) |
| (6.6) |
Now we can calculate Maxwell currents in case of radial potential:
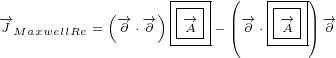 |
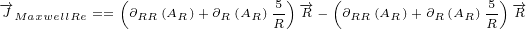 |
 |
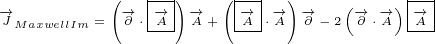 |
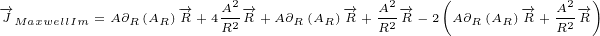 |
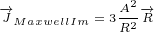 |
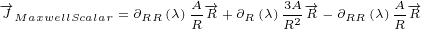 |
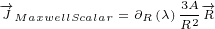 |
For radial potential, Maxwell real current iz zero, but Maxwell imaginary current and
Maxwell scalar current are not zero.
We can say that Maxwell imaginary current and Maxwell scalar current are not radially
symmetric.
7 Analyzing Maxwell scalar current
Let us write this equation:
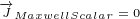 |
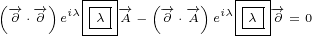 |
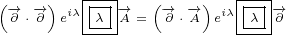 |
I will solve it in most simple case, when we have only 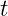 and
and  parameters:
parameters:
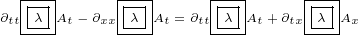 |
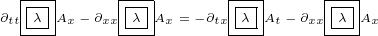 |
We can cancel some terms and write:
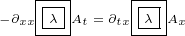 |
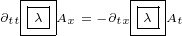 |
Then we can switch sides for second equation:
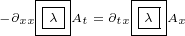 |
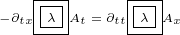 |
Now we can divide left and right hand sides. That will remove 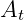 and
and 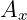 terms, so
terms, so
only scalar term 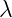 will remain:
will remain:
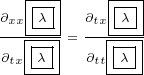 |
Finally we can write:
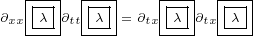 |
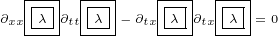 |
I think same procedure can be used in general case, when all parameters, 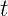 ,
, 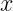 ,
, 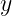
and 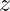 are present.
are present.
8 Conclusion
4D multivector reflection equation can be used to describe Maxwell equations in very concise
and elegant way. Based on this fact, I have tried to show that 8D multivector reflection
equation can be used to create something that we can call Maxwell equations in
8D.
The results are very interesting. We have defined new entities. We have defined Maxwell
real current, Maxwell imaginary current and Maxwell scalar current.
Maxwell imaginary current must be analayzed in more depth. When Maxwell real
current is taken to be zero, we get equation that describes electromagnetic waves. It would
be very interesting to find some solutions for the following equation, that we get when
Maxwell imaginary current is taken to be zero:
 |
Further analysis is needed for the Maxwell scalar current. It seems that we can get rid of
potential vector 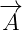 entirely, which would leave only one equation with scalar term
entirely, which would leave only one equation with scalar term
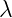 .
.
A Proof for reflections in 3D
For this section we will use following notation: for 3D vectors we will use upper case letters
and for components we will use lower case letters. For the geometric product we will use 
symbol.
So, we can write:
![N∘V ∘N =(nx,ny,nz)(vx,vy,vz)(nx,ny,nz)
(|(nxvx +nyvy +nzvz))|( )
N ∘V ∘N =|( ((nnxvyvyz-- nnyvzvxy)x)yyz |) nx,ny,nz
( (nzvx- nxvz)zx )
|| (n2xvx+nxnyvy+ nxnzvz+nx(.n..y)yvy- n2yvx- n2zvx+nxnzvz)x||
N ∘V ∘N =||( (...)z ||)
(nxnzvy- nynzvx+ nxnyvz- nxnzvy +nynzvx- nxnyvz)xyz
( (n2xvx+2nxnyvy+ 2nxnzvz- n2yvx- n2zvx)x)
N ∘V ∘N =|||| (.(.....)y)z ||||
( (0)xyz )
( 2 2 2 2 )
N ∘V ∘N = ||(2nxvx +2nxnyvy+2nxn(.zv..z)y- nxvx- nyvx- nzvx)x||
( (...)z )
( [2(N ⋅V)nx- N2vx]x)
N ∘V ∘N =||( [2(N ⋅V)ny- N22vy]y||)
[2(N ⋅V)nz- N vz]z
N∘V ∘N = 2(N ⋅V )N - N2V
N ∘V ∘N = 2(N⋅V)N- (N ⋅N)V](/images/Maxwell387x.png) |
(A.1)
(A.2) (A.3) (A.4) (A.5) (A.6) (A.7) (A.8) |
We can write this in different form:
| (A.9) |
Left hand side is a vector, since we have only scaling and subtraction operations.
Looking at the right hand side we can say that length of this new vector is equal to 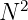
multiplied by length of V. We can say this, because geometric product preserves
lengths.
So, finally we can write our reflection equation that reflects vector V to vector
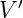 :
:
| (A.10) |
A.1 Continuity equation
We can identify vector J:
| (A.11) |
We can easily prove that vectors N and J are perpendicular:
| (A.12) |
| (A.13) |
A.2 Gauge transformation
Let us define gauge transformation of vector V as translation of vector V along direction of
vector N:
| (A.14) |
We can now prove that gauge transformation does not change vector J:
| (A.15) |
| (A.16) |
| (A.17) |
| (A.18) |
All these equations from Annex A are easy to prove and visualize for 3D case.
What is remarkable is that these equations can be applied for general case of
multivector which has 8 components (1 scalar, 3 vectors, 3 pseudovectors and 1
pseudoscalar)!
This we are going to prove in Annex B and Annex C!
B Proof for reflections in 4D
For this section we will use following notation: for 4D multivectors we will use upper case
letters and for scalars and 3D components we will use lower case letters.
So, we can write:
| (B.1) |
| (B.2) |
Let us also define scalar product for 4D multivectors as:
| (B.3) |
| (B.4) |
And let us define conjugate 4D multivector as:
| (B.5) |
We can begin our proof by writing geometric product similar to 3D case:
| (B.6) |
For 3D vectors we have:
| (B.7) |
| (B.8) |
So, we can continue:
| (B.9) |
We can write this in different form:
| (B.10) |
Left hand side is a 4D multivector, since we have only scaling and subtraction
operations.
Looking at the right hand side we can say that length of this new 4D multivector
is equal to 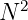 multiplied by length of V. We can say this, because geometric
multiplied by length of V. We can say this, because geometric
product preserves lengths, and length of vector 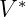 is the same as length of vector
is the same as length of vector
V.
So, finally we can write our reflection equation that reflects 4D multivector V to
paravector 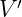 :
:
| (B.11) |
Continuity equation and gauge transformation that we defined in Annex A for 3D case,
can also be proved here for 4D case. Prove is exactly the same, so no need to repeat it here.
We can just write them.
Here is continuity equation for 4D case:
| (B.12) |
And here is gauge transformation for 4D case that does not change multivector
S:
| (B.13) |
C Proof for reflections in 8D
General multivector has 8 components – 1 for scalar, 3 for vector, 3 for pseudovector and 1
for pseudoscalar.
It is easier to think of 8D multivector as sum of two 4D multivectors:
| (C.1) |
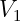 and
and 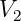 are 4D multivectors, and
are 4D multivectors, and 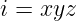 is pseudoscalar.
is pseudoscalar. 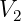 is multiplied
is multiplied
by 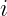 , so it contains pseudovector and pseudoscalar components of multivector
, so it contains pseudovector and pseudoscalar components of multivector
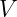 .
.
We can keep N and S symbols the same as in 3D and 4D case, but note that they also
are 8D multivectors (they also can be written as sum of two 4D multivectors).
Equation for scalar product of two 8D multivectors can be written by using scalar
product of 4D multivectors:
| (C.2) |
| (C.3) |
| (C.4) |
| (C.5) |
We are ready to prove reflection equation for 8D case:
| (C.6) |
Let us pause here. First few terms that are on the left side have 4D geometric products of
4D multivectors that we can expand using equation from Annex B. But terms on the right
side have geometric products of three diferent 4D multivectors, so we cannot apply equation
from Annex B in that case.
So, let us check how does geometric product of three different 4D multivectors looks like:
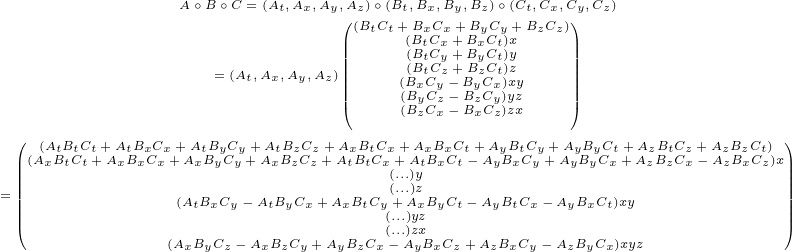 |
(C.7)
(C.8) (C.9) |
Scalar 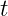 component part can be written as:
component part can be written as:
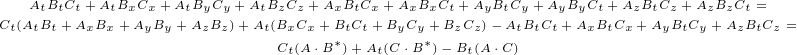 |
(C.10)
(C.11) (C.12) |
Vector 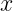 component part can be written as:
component part can be written as:
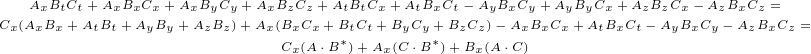 |
(C.13)
(C.14) (C.15) |
Based on the fact that scalar and vector parts are symmetric and pseudescalar and
pseudovector parts are anti-symmetric, we can now write:
![A ∘ B ∘C + C ∘B ∘ A = 2[C(A ⋅B *)+ A (C ⋅B*) - B*(A ⋅C )]](/images/Maxwell433x.png) |
(C.16) |
Now we can continue our proof:
| (C.17) |
We can write this in different form:
| (C.18) |
Looking at the right hand side we can say that length of this new 8D multivector is
equal to 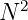 multiplied by length of
multiplied by length of 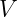 . We can say this, because geometric
. We can say this, because geometric
product preserves lengths, and length of vector 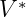 is the same as length of vector
is the same as length of vector
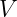 .
.
So, finally we can write our reflection equation that reflects 8D multivector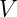 to 8D
to 8D
multivector 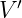 :
:
| (C.19) |
Continuity equation and gauge transformation that we defined in Annex A and B for 3D
and 4D case, can also be proved here for 8D case. Prove is exactly the same, so no need to
repeat it here. We can just write them.
Here is continuity equation for 8D case:
| (C.20) |
| (C.21) |
And here is gauge transformation for 8D case that does not change vector
J:
| (C.22) |
Here we have used symbol 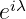 as multivector scalar, that has scalar and pseudoscalar
as multivector scalar, that has scalar and pseudoscalar
term.

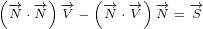
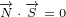
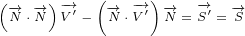
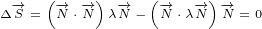
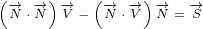
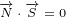
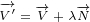
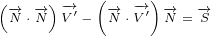
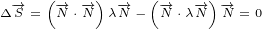
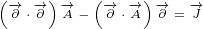
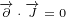
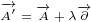
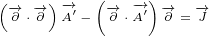
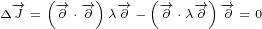
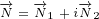
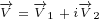
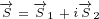
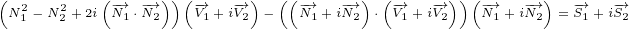
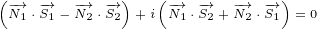
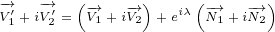
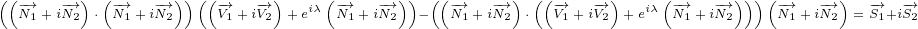
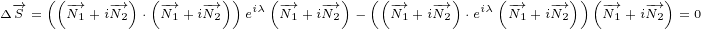
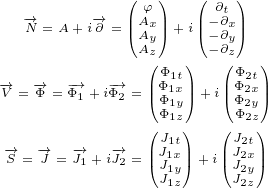
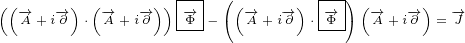
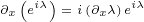
![( ) [ ]
∂xx eiλ = ∂x i(∂xλ)eiλ](/images/Maxwell150x.png)
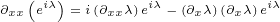
![( ) [ ]
∂xy eiλ = ∂y i(∂xλ)eiλ](/images/Maxwell152x.png)
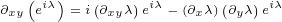
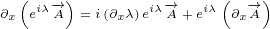
![( ) [ ( )]
∂xx eiλ-→A =∂x i(∂xλ)eiλ-→A+ eiλ ∂x-→A](/images/Maxwell155x.png)
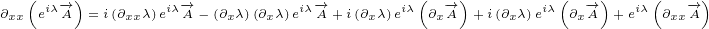
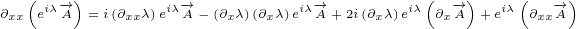
![( iλ-→) [ iλ-→ iλ( -→ )]
∂xy e A =∂y i(∂xλ)e A+e ∂xA](/images/Maxwell158x.png)
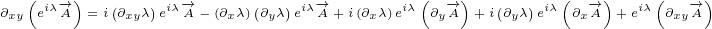
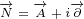
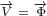
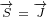


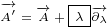
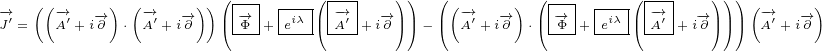
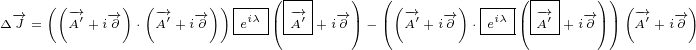
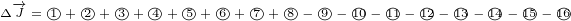
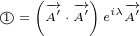
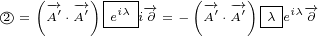
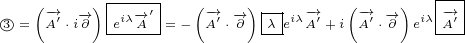
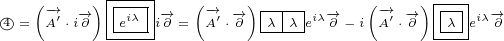
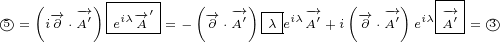
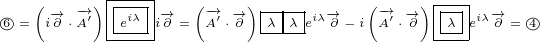
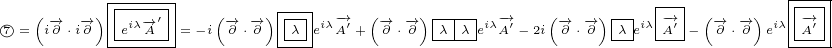
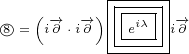
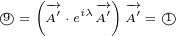
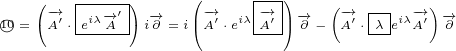
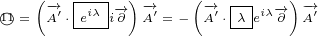
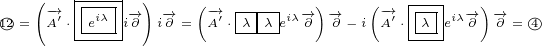
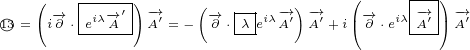
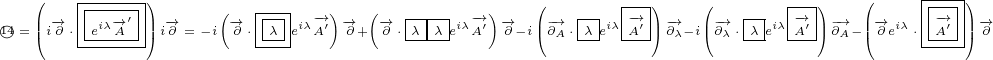

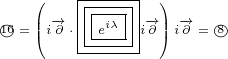

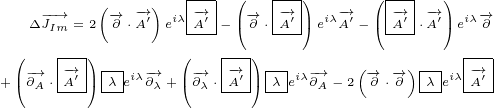
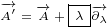
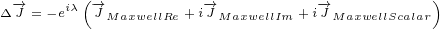
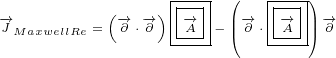
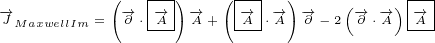
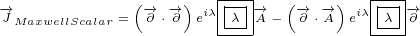
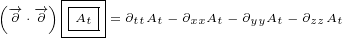
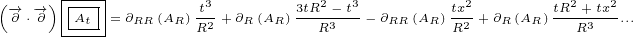
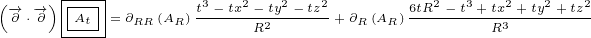
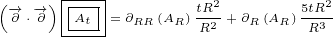
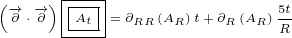
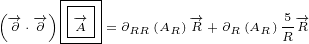
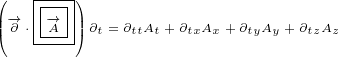
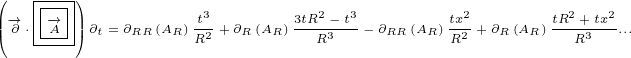
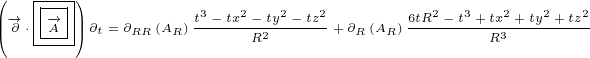
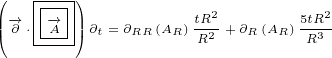
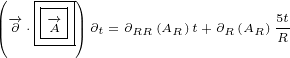
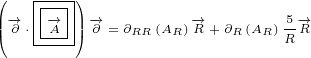
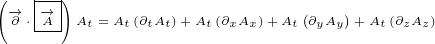
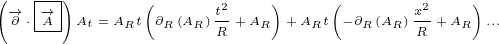
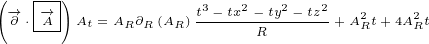
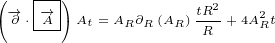
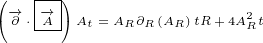
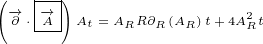
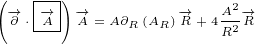
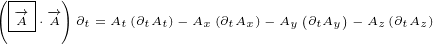
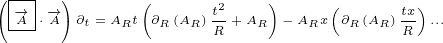
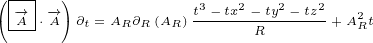
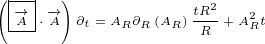
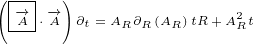
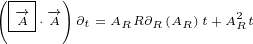
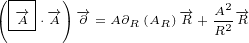
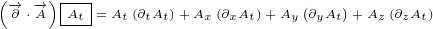
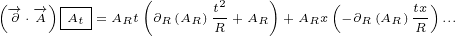
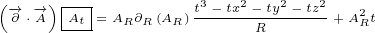
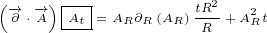
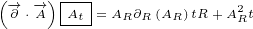
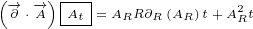
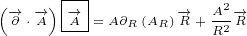
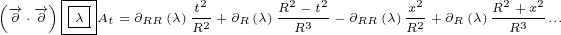
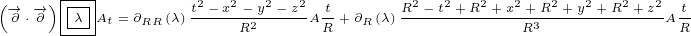
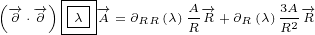

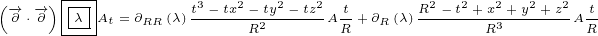
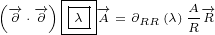
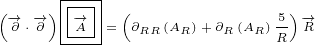
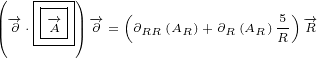
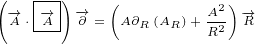
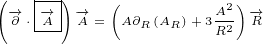
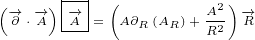
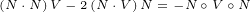
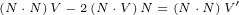
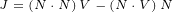
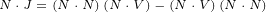
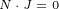
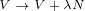
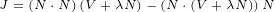
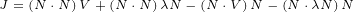
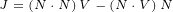
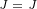
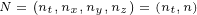
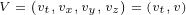
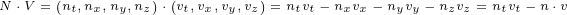
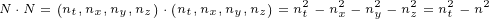
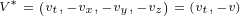
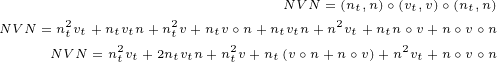
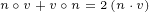
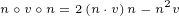
+2n vt+22(n ⋅v2)n- n2v]
N ∘V ∘N = 2ntvt+2ntvtn+2nt(n ⋅v)+2(n⋅v)n + -[ntvt+ntv+n vt- nv]
N∘V ∘N = [2nt(ntvt+ n⋅v)+ 2n (ntvt+ n⋅v)]+ -n2t(vt,-v)+n2(vt,-v)
N∘V ∘N = [2nt(N⋅V*)+2n(N⋅V*)]+ [-n2tV*+ n2V*]
N ∘V ∘N =2(N⋅V*)N - N2V*
N ∘V ∘N =2(N ⋅V*)N - (N⋅N)V*](/images/Maxwell408x.png)
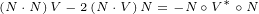
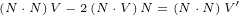
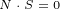
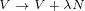
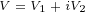
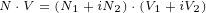
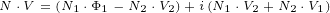
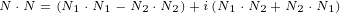
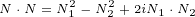
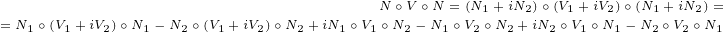
![N ∘V ∘N = (N + iN )∘(V + iV )∘(N +iN )=
= N1∘(V1+ iV2)∘N1- N2∘(V1+iV2)∘N2 +iN1 ∘V1 ∘N2- N1∘V21∘N2 2+iN2 1∘V1∘2N1- N12∘V2∘2N1
= -N2(V*+iV*)+2[(V* +iV*)⋅N1]N1- (iN2)2(V *+iV*)+ 2[(V*+ iV*)⋅iN2]iN2
1 1 2 +1i(N12∘V1∘N2+ N2∘V1∘N11)- (N21 ∘V2∘N12+N22∘V2∘N1)=
- (N2- N2)(V* +iV *)+ 2[(V*+iV*)⋅N1]N1- 2[(V*+ iV*)⋅N2]N2
+2i[(V* ⋅N )N + (V*⋅N )1N - (2N ⋅1N )V2*]- 2[(V*1⋅N )2N +(V*⋅N )N 1- (N 2⋅N )V*]=
1 1 2 1 2( 21 21)(*2 1 *) [(2* 1 *2) ]2 2 [(1* 1*)2 2]
[( * ) ( * - N)1 - N2 V1 +iV2* +(2*V1 +)iV2 ⋅N(1*N1-)2 V1 + iV2 ⋅N2*N]2
( 2 2)( +*2i V*1) ⋅N1[(N2*+ V1* ⋅)N2 N1- (N]1⋅N2)V1[( +*iV2*⋅N)1 N2+ iV2] ⋅N2 N1- i(N1⋅(N*2)V2)=
- N1 - N 2 V1 + iV2 +2 V1 +iV2 ⋅(N1+iN2)[N1- 2 V1 + iV2 ⋅(N2]- iN1) N2- (N1⋅N2)2iV1 ⋅N1 =
- N21 - N22 +2i(N *1 ⋅N2) V*+ 2(V*⋅N)N1+ 2i(V*⋅N)N2 =
-N2V*+2(N ⋅V*)N](/images/Maxwell434x.png)